While the term “diagrammatic higher category” is new, its underlying idea is not: coherences in higher structures can be derived from (stratified) manifold topology. This idea is central to the cobordism hypothesis (and to the relation of manifold singularities and dualizability structures as previously discussed on the $n$-Café), as well as to many other parts of modern Quantum Topology. So far, however, this close relation of manifold theory and higher category theory hasn’t been fully worked out. Geometric higher category theory aims to change that, and this blog post will sketch some of the central ideas of how it does so. A slightly more comprehensive (but blog-length-exceeding) version of this introduction to diagrammatic higher categories can be found here:
Today, I only want to focus on two basic questions about diagrammatic higher categories: namely, what is the idea behind the connection of geometry and higher category theory? And, what are the first ingredients needed in formalizing this connection?
What is geometric about diagrammatic higher categories?
I would like to argue that there is a useful categorization of models of higher structures into three categories. But, I will only give one good example for my argument. The absence of other examples, however, can be taken as a problem that needs to be addressed, and as one of the motivations for studying diagrammatic higher categories! The three categories of models that I want to consider are “geometric”, “topological” and “combinatorial” models of higher structures. Really, depending on your taste, different adjectives could have been chosen for these categories: for instance, in place of “combinatorial”, maybe you find that the adjectives “categorical” or “algebraic” are more applicable for what is to follow; and in place of “geometric”, maybe saying “manifold-stratified” would have been more descriptive.
But let’s get to the promised example of how these three categories of models work and how they relate. We start with the archetypical model of a type of higher structure: namely, with topological spaces. Unsurprisingly, topological spaces fall firmly into the category of topological models. The type of higher structure modelled by topological spaces deserves a name: we will refer to them as homotopy types. There is a second well-known model for homotopy types, namely, $\infty$-groupoids. Unlike spaces, whose theory is based on the continuum $\mathbb{R}^n$, $\infty$-groupoids are discrete structures whose data is captured by collections of morphisms in each dimension $k \in \mathbb{N}$. This makes $\infty$-groupoids a prime example of a ‘combinatorial’ (or, ‘algebraic’, or, ‘categorical’) model of a higher structure. (I should point out that I am being vague about concrete definitions of the above named ‘models’; for instance, ‘spaces’ could be, more concretely, taken to mean CW complexes, and $\infty$-groupoids could be taken to mean Kan complexes.) Despite being rather different in flavour, the higher theory (i.e. the homotopy theory) of topological spaces and the higher theory of $\infty$-groupoids turn out to be equivalent. The two models are related by two important constructions: we can pass from spaces to $\infty$-groupoids by taking the fundamental categories of spaces (usually referred as their ‘fundamental $\infty$-groupoids’), and, conversely, we can realize $\infty$-groupoids as spaces.
Now the interesting question: what is the geometric counterpart to the above topological and combinatorial models? In different words, how can we understand the homotopy theory of spaces in terms of a theory of manifold-stratified structures? The answer is given by the theory of cobordisms, or more precisely, stratified cobordism. The most well-known instance of how cobordisms and spaces relate in this sense is the classical Pontryagin theorem. The theorem describes the isomorphism $\Omega ^{\mathrm{fr}} _{m} (\mathbb{R} ^{n})$ $\cong$ $\pi _{n} (S ^{n-m})$ between the cobordism group of smooth (normal) framed $m$-manifolds in $\mathbb{R}^n$ and the $n$th homotopy group of the $(n-m)$-sphere. The resulting relation between smooth manifold theory and homotopy theory is incredibly ubiquitous in modern Algebraic Topology (and, relatedly, in Physics) but often implicitly so—in the words of Mike Hopkins, Pontryagin’s theorem itself marks the point in time at which Algebraic Topology became ‘modern’.
Importantly for us, the theorem generalizes from spheres to arbitrary spaces (or, more precisely, CW complexes): namely, the $n$th homotopy group of any space can be understood in terms of framed stratified cobordisms group of framed compactly supported manifold stratifications of $\mathbb{R}^n$. The details of this generalization are spelled out in [1,§VII], in a chapter titled “the geometry of CW complexes”, but really the basic idea of the construction remains essentially the same (for the experts: instead of working with regular points of the sphere $S^{n-m}$, we work with regular regular dual stratifications of CW complexes). To summarize, we can study the homotopy groups of spaces, or, in combinatorial terms, the higher morphisms in $\infty$-groupoids, by means of framed stratified cobordisms in $\mathbb{R}^n$. The relation between the geometry of stratified cobordisms and the homotopy theory of spaces can be conceptually thought of as a two-step process of ‘dualizing globalization’: this comprises dualization (which translates stratification data back into cells, and we will return to this later on) and globalization (which glues cells to obtain spaces).
The main point I now want to make is that the trilogy of geometric, topological, and combinatorial models exemplified above in the case of homotopy types should also extend to other types of higher structures. In particular, $(\infty,1)$-categories and $(\infty,n)$-categories should admit both topological models and geometric models—however, these classes of models haven’t been much explored so far (as an aside, in the $(\infty,1)$-case there is the theory of $d$-spaces which I will count as an existing topological counterpart to $(\infty,1)$-categories even though I’m unsure how much this relation has been formally explored). The situation is summarized in Table 1 below, in which we have filled in precisely some of the missing entries for geometric and topological models of higher structures: to indicate their conceptual nature, names of these models have been kept in quotes.
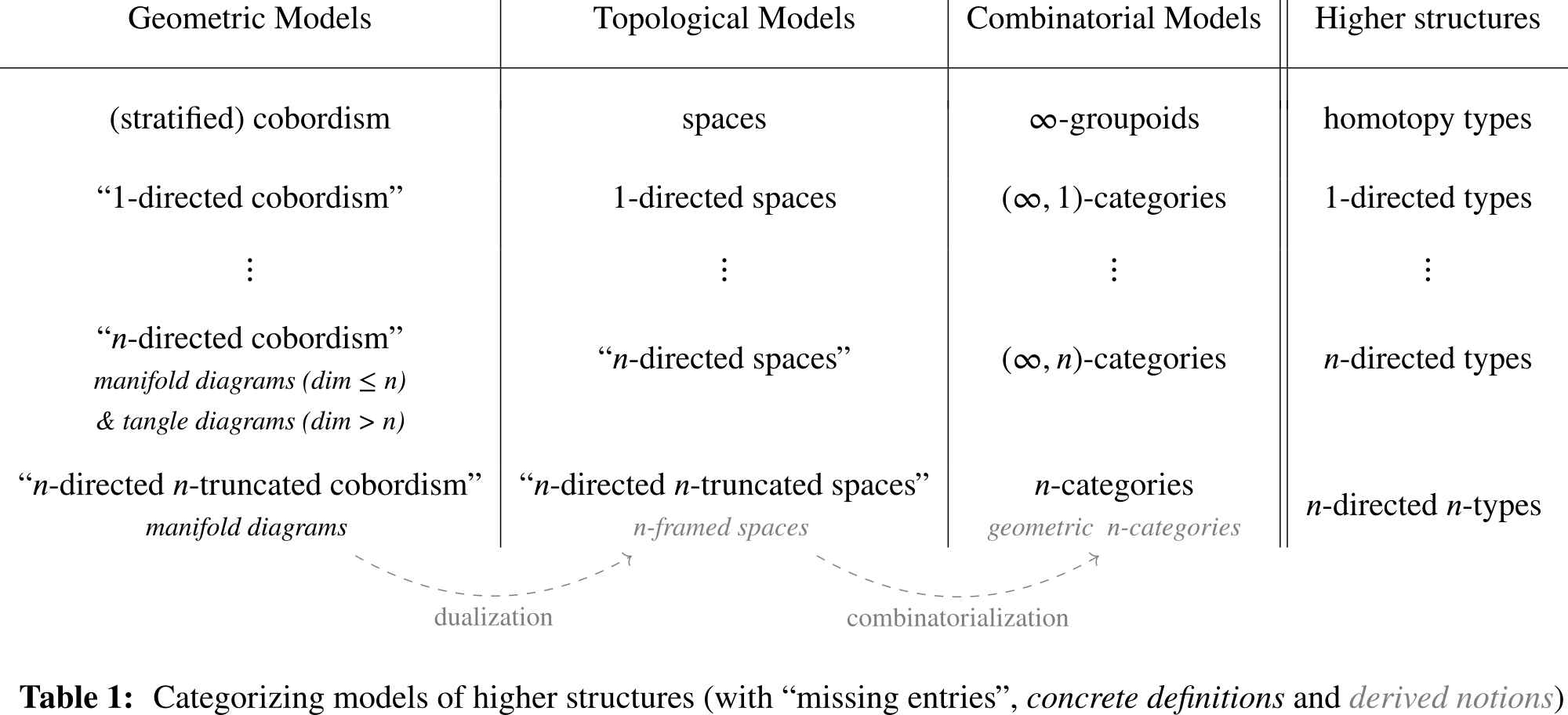
At a first glance, it seems like finding concrete definitions for these directed geometric models would be a tall order. After all, the theory of stratified cobordisms itself has its mathematical depths, and realizing the step from $\infty$-groupoids (say, Kan complexes) to concrete definitions of $(\infty,n)$-categories is not necessarily an obvious one.
But this is where things may get exciting. Indeed, by the end of this blog post I hope to have convinced you that the geometric models of higher structures may, in fact, get much easier when passing to the directed setting of $n$-categories. Moreover, to then study the undirected setting (i.e., in combinatorial terms, the case of higher categories with invertible morphisms) from the perspective of directed geometric models provides a refined view on the computational intricacies of invertibility.
Of course, in order to be able to tell this story, I will have to shortly show you some concrete notions that aim to realize the geometric models outlined above. The notions go by the names manifold diagrams resp. tangle diagrams, the latter being the relevant notion in the undirected case. Both terms have been added to Table 1 in their respective places (note that the $(\infty,n)$-case requires us to deal with manifold diagrams in and below dimension $n$, and with tangle diagrams above dimension $n$). Importantly, note that I wrote that these notions ‘aim to realize’ the aforementioned geometric models. Indeed, how do we measure ‘correctness’ of our definitions of manifold diagrams? Unfortunately, no reasonably-straight-forward benchmark for models of directed geometry exists at this point (actually, the same was true for manifolds when they were discovered, but they were quickly accepted due to their ubiquity in mathematics and physics). Certainly, passing from geometry to combinatorics in Table 1, a comparison to existing models of $(\infty,n)$-categories would provide such a benchmark, but it also turns out to be substantial work due to some fundamental differences of how the notion of coherence is conceived (nonetheless, Lukas Heidemann is a PhD student at Oxford who is actively thinking about this question!). For today, instead of such a comparison, I would like to argue that the geometric models of higher structures deserve your interest for the following set of more elementary reasons.
-
Simplicity and ubiquity. Firstly, the definitions of manifold and tangle diagrams are simultaneously simple and expressive: both definitions succeed in encompassing large classes of known examples, including ordinary string diagrams and surface diagrams, knot and surface-knot diagrams, as well as their respective moves (Reidemeister move and ‘movie moves’), and smooth manifold singularities such as Arnold’s ADE singularities [2].
-
Trilogy of models. Secondly, and this is a central part of the story, both manifold and tangle diagrams have canonical topological and combinatorial representations. This enables a powerful translation between all three columns of Table 1: in the topological column this translation results in a local model of directed space termed framed spaces, and in the combinatorial column it yields, you guessed it, diagrammatic higher categories. In this combinatorial model, higher-categorical coherences are then naturally related to stratified manifold isotopies!
-
Application. Thirdly and lastly, even without higher structures as our primary object of study, manifold and tangle diagrams provide a new tool at the interface of combinatorial higher algebra and differential topology. This might (or might not) be interesting especially in dimension 4 where some aspects of the theory of smooth structures remain mysterious.
So we now have a rough idea about what makes diagrammatic higher categories ‘geometric’, and why they might be interesting. Next, let’s see some manifold diagrams!
From zero to manifold diagrams
Here’s a one-line slogan about manifold diagrams: manifold $n$-diagrams are compactly triangulable, conical stratifications of $n$-dimensional directed euclidean space. There are thus three ingredients that we need to talk about.
-
What is ‘directed euclidean space’?
-
What are (conical) stratifications?
-
What does it mean to be compactly triangulable?
Let’s address these ingredients in the above order!
Ingredient 1: Directedness via framings
We will infuse our spaces with directions by means of framings: recall, classically, a framing is something akin to a ‘choice of tangential directions’ at all points of a given space (usually a manifold, as otherwise it may be hard to talk about ‘tangential directions’). Our use of the term ‘framing’ will be a somewhat non-standard variation of this idea. For motivation, we start with the observation that given a real $n$-dimensional inner product space $V$, the following two structures on $V$ are equivalent: firstly, the choice of an orthonormal framing of $V$, i.e. an ordered sequence $(v_1, v_2, …, v_n)$ with $\langle v_i, v_j \rangle = \delta_{ij}$, and, secondly, a chain of linear surjections $V_i \to V_{i-1}$ of orientied $i$-dimensional $V_i$’s starting at $V_n = V$. A correspondence between these structures can be produced by defining $V_i = \mathrm{span}(v_1, …, v_i)$ with $V_i \to V_{i-1}$ forgetting $v_i$. To get a bit of intuition about what’s going on here, let’s consider the following analogous and hopefully familiar situation: given a Riemannian manifold $M$ there is a correspondence between (smooth) gradient vector fields on $M$ and (smooth) functions $M \to \mathbb{R}$ up to shifting functions by a constant. (To ensure the analogy is clear: the vector field, where it is non-zero, plays the role of a 1-frame $v_1$, whereas the corresponding function $M \to \mathbb{R}$ plays the role of a linear surjection $V \to V_1$ of tangent spaces at these points.) So why would we want to shift perspectives from vectors to surjections in this way? The secret reason is that ‘orthonormality’ ceases to exist in absence of inner products (or, in the given analogy, in absence of Riemannian metrics), but the notion of linear surjections does not. Put differently, by basing our notion of framings on surjections rather than vectors we can emulate some form of orthnormality even in the absence of inner products (cf. [3, App. A]). Somehow, this is rather important for the story of manifold diagrams. But let’s put the intuition aside, and spell out the definition.
While it is possible to use the above idea of ‘framings-via-surjection-towers’ to define framed spaces in quite some generality, we will only be interested in the euclidean case (this case is in some sense a ‘local model’ for more general framed spaces). Here it is: the standard $n$-framing of $\mathbb{R}^n$ is the chain of oriented $\mathbb{R}$-fiber bundles $\pi_i : \mathbb{R}^i \to \mathbb{R}^{i-1}$ ($1 \leq i \leq n$) with $\pi_i$ defined to be the map that forgets the last coordinate of $\mathbb{R}^i$ (and with fibers carrying the standard orientation of $\mathbb{R}$ after identifying $\mathbb{R}^i = \mathbb{R}^{i-1} \times \mathbb{R}$). When considering $\mathbb{R}^n$ we will always tacitly think of it as ‘standard framed $\mathbb{R}^n$’ and, thus, we stop mentioning the standard framing as an explicit structure all-together. Indeed, more important than defining the standard $n$-framing is to define the maps that preserve it: a framed map $F : \mathbb{R}^n \to \mathbb{R}^n$ is a map for which there exist (necessarily unique) maps $F_j : \mathbb{R}^j \to \mathbb{R}^j$ ($0 \leq j \leq n$) with $F_n = F$ such that $\pi_i \circ F_i = F_{i-1} \circ \pi_i$ with $F_i$ preserving orientations of fibers of $\pi_i$ (for concreteness, let’s take ‘orientation preserving’ to mean strictly monotonic).
How to such framed maps look like? Well, you can think up examples in an inductive fashion. A framed map $\mathbb{R} \to \mathbb{R}$ is simply a stricty monotonous one. Next up, a framed map $\mathbb{R}^2 \to \mathbb{R}^2$ is a map that descends along $\pi_2 : \mathbb{R}^2 \to \mathbb{R}$ to a framed map $\mathbb{R} \to \mathbb{R}$, and also maps fibers of the projection strictly monotonicly… and so on. From this, it’s not so hard to deduce a first basic observation: the space of framed homeomorphism $\mathbb{R}^n \to \mathbb{R}^n$ is, in fact, contractible.
Ingredient 2: Conical stratifications
Next up, let’s discuss stratifications. Really, the only thing you need to know is the following. In its weakest form, a stratification $f$ of a space $X$ (together also called a ‘stratified space’ $(X,f)$) is a decomposition of that space into a disjoint union of subspaces called strata. And a stratified map of stratified spaces is a map of underlying spaces that maps strata of the domain into strata of the codomain (a ‘stratified homeomorphism’ is a stratified map with an inverse stratified map). Products of stratified spaces take products of underlying spaces and stratify them with products of strata. Cones of stratified spaces take products of underlying spaces and stratify them with cones of strata, but the cone point is kept as a separate stratum.
Simple enough! But, if you happen to have an inclination towards higher structures, then I can easily relay a better way of thinking about stratifications in a single sentence: namely, spaces are to sets, what stratifications are to posets. The situation is illustrated in Table 2 (non-standard terminology is kept in quotes as before). In particular, just as spaces $X$ have fundamental sets $\pi _ 0 X$, stratifications have fundamental posets $\mathsf{E} _ 0 X$. Just as spaces $X$ have fundamental $\infty$-groupoids $\Pi_\infty X$, and both $X$ and $\Pi_X$ model the same homotopy type, stratifications have fundamental $\infty$-posets $\mathsf{E} _ \infty X$, and both model the same higher structure. (Here ‘$\mathsf{E}$’ indicates that in the literature one more commonly finds the terms ‘Entrance’ or ‘Exit path categories’; but really, there’s a general story to be told here for passing from an structure S to an $\infty$-S structure, and from a topological thing to its fundamental category, so ‘fundamental $\infty$-poset’ is not a bad name at all and it illustrates the point.) Importantly, to make this higher-categorical story work nicely, it turns out to be central that our topological definition of stratified spaces has one further property: conicality!

While both conicality and the aforementioned higher-categorical constructions are discussed in more detail in the extended version of this post, here, we shall not need them in full generality. Indeed, we are only interested in the framed euclidean case, and that case goes as follows. First note that the adjectives ‘framed’ and ‘stratified’ can be easily combined: for instance, a framed stratified map $(\mathbb{R}^n,f) \to (\mathbb{R}^n,g)$ is a stratified map whose underlying map $\mathbb{R}^n \to \mathbb{R}^n$ is framed. Moreover, when working with stratified products $(\mathbb{R}^k,f) \times (\mathbb{R}^{n-k}, g)$ we will identitify $\mathbb{R}^n \cong \mathbb{R}^k \times \mathbb{R}^{n-k}$ in the standard way; and, when working with stratified cones $(\mathrm{Cone}(S^{n-1}), \mathrm{cone}(l))$ of stratified spaces $(S^{n-1}, l)$, we will standard embed $S^{n-1} \hookrightarrow \mathbb{R}^n$ and identify $\mathrm{Cone}(S^{n-1}) \cong \mathbb{R}^n$ by mapping $(x \in S^{n-1},\lambda \in [0,1))$ to $\frac{\lambda}{1 - \lambda}x \in \mathbb{R}^n$. With these conventions at hand, we may now introduce conicality in our framed setting as follows: a stratification $(\mathbb{R}^n,f)$ is framed conical if each point $x \in \mathbb{R}^n$ it has a framed stratified neighborhood which is framed stratified homeomorphic to $\mathbb{R}^k \times (\mathrm{Cone}(S^{n-k-1}), \mathrm{cone}(l))$ with $x \in \mathbb{R}^k \times {0}$, where $0 \leq k \leq n$ and $(S^{n-1}, l)$ is some stratification. Importantly, framed conicality is really just a ‘framed’ version of traditional conicality!
Ingredient 3: Framed compact triangulability
The last ingredient for the notion of manifold diagrams is that of framed compact triangulability. To begin, let me remark that imposing a compact triangulability condition is a reasonable thing to do: indeed, in our earlier discussion of Pontryagin’s theorem we similarly met cobordisms of manifolds embedded in $\mathbb{R}^n$ that always have compact support—’framed compact triangulability’ may be thought of as a generalization of this situation (adapted to the setting of framed stratified spaces). The condition can be succinctly formulated by starting in the PL category: a compactly-defined triangulation $K$ of $\mathbb{R}^n$ is a finite stratification of $\mathbb{R}^n$ by open disks whose closures are the images of linear embeddings $\Delta^k \times \mathbb{R}^l_{\geq 0} \hookrightarrow \mathbb{R}^n$ ($k + l \leq n$). This translates to the framed stratified case as follows: a stratification $(\mathbb{R}^n,f)$ is framed compactly triangulable if it admits a framed stratified subdivision $(\mathbb{R}^n,K) \to (\mathbb{R}^n,f)$ of $f$ by a compactly-defined triangulation $K$. (I believe the word ‘subdivision’ is self-explanatory, but in case it is not: a stratified subdivision is a stratified map whose underlying map is a homeomorphism.)
Putting it all together
We have now introduced all the necessary ingredients (and importantly, there are not that many), and we can mix them together in the following central definition.
Definition. A manifold $n$-diagram is a framed conical stratification $(\mathbb{R}^n,f)$ that is framed compactly triangulable.
Let’s unwind this definition and look at some examples. First, in order to be able to depict $\mathbb{R}^n$, observe that there is a framed homeomorphism $\mathbb{R}^n \cong _{\mathrm{fr}} (-1,1) ^n$; here, ‘framed’ means that composing with the inclusion $(-1,1) ^n \hookrightarrow \mathbb{R}^n$ yields a framed map $\mathbb{R}^n \to \mathbb{R}^n$ as defined earlier (in fact, the choice for a framed identification $\mathbb{R}^n \cong _{\mathrm{fr}} (-1,1) ^n$ is again unique up to contractible choice). With that in mind, we will depict all our examples of manifold diagrams as living on the open cube $(-1,1)^n$.
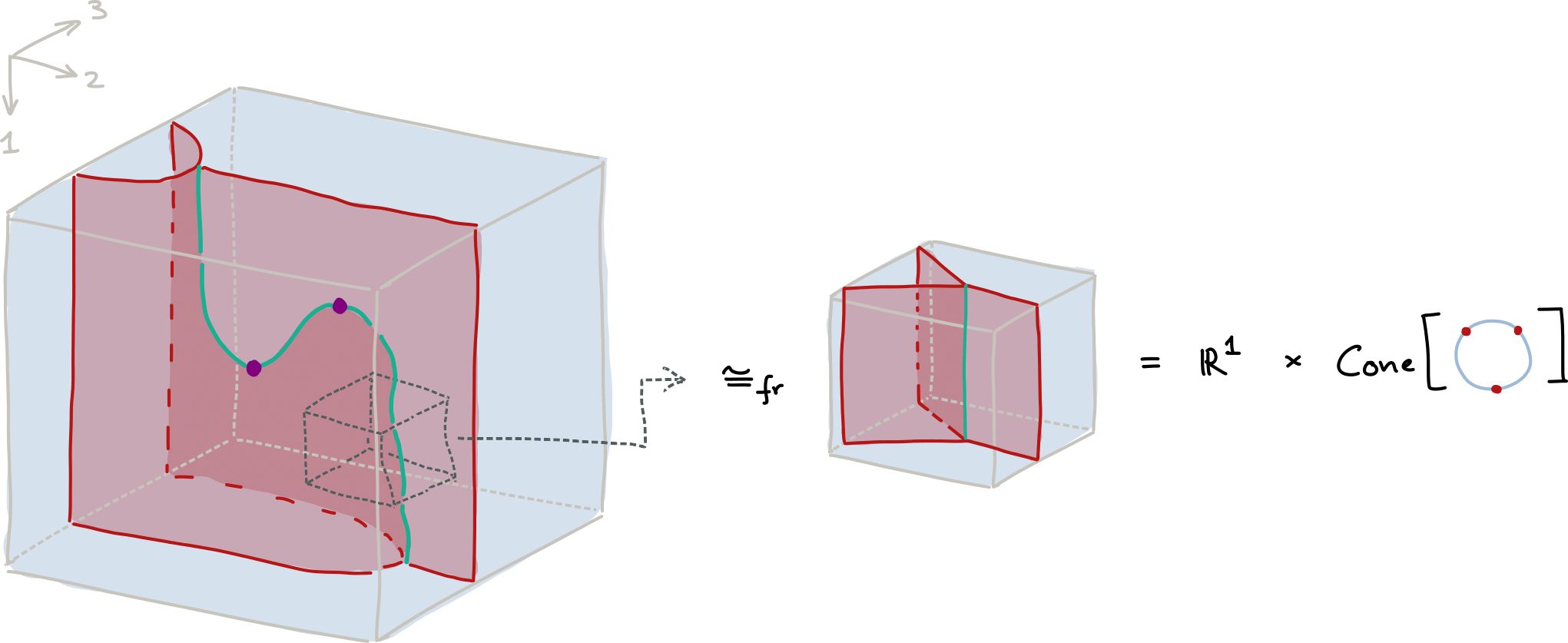
- Example 1: String diagrams. An ordinary string diagram is a manifold 2-diagram. We illustrate one in Figure 1 below, and visually verify the framed conicality condition at two points.
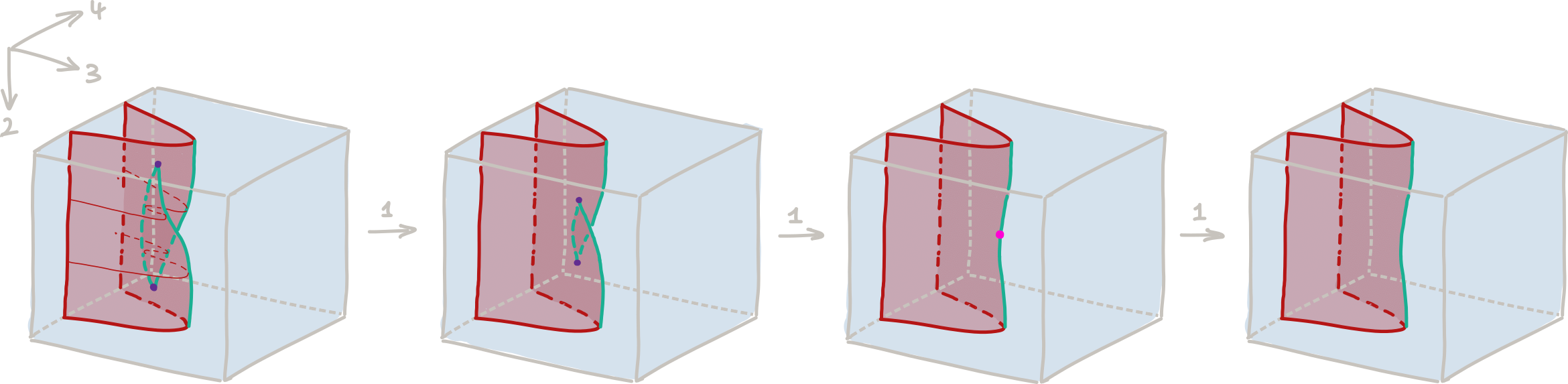
- Example 2: The ‘Cockett pocket’ law (Verity). This is a 3-manifold diagram shown in Figure 2 below. We indicate a couple of tubular neighborhoods as before.
-
Example 3: The link of the swallowtail singularity. It is often useful to think of a manifold $n$-diagram as a ‘movie’ of manifold $(n-1)$-diagrams. As an example, check out this $n$Lab picture which illustrates a manifold 3-diagram as a movie of manifold 2-diagrams (note that diagram is ‘stratified by the named strata’; for instance, the surface labelled by $U$ is its own stratum, and so is the line stratum labeled by $\epsilon$ etc.). Bonus trivia fact: the picture happens to be the title image of MSRI program 323 “Higher categories and categorification”.
-
Example 4: The Reidemeister III isotopy. In one dimension up, we find yet new behaviour captured by manifold diagrams. For instance, the Reidemeister III isotopy is the (track of an) isotopy that shifts a constellation of three braids into a different constellation of three braids, while passing through a triple braid. This is illustrated in this $n$Lab picture and it, too, is a manifold diagram as can be easily verified!
The first few properties
Let us mention a few important consequences of our definition of manifold diagrams, some of which link back to our earlier question of why one may want to care about manifold diagrams, and others which highlight some of the pleasant properties of manifold diagrams (the verifications of all these consequences can be found in [4]).
-
While the compact triangulability condition requires the existence of some combinatorial representation (i.e. triangulation), it turns out that there is in fact a canonical combinatorial representation for manifold diagrams (up to framed stratified homeomorphism). Maybe it is helpful to give just one more sentence of condensed explanation here: this property follows from the observation that manifold diagrams have universal framed subdivisions by framed stratified homotopy 0-types called meshes, which (after passing to the ‘framed fundamental posets’ of meshes) leads us to a combinatorial notion called trusses—trusses (endowed with appropriate combinatorial stratification data) then combinatorially classify manifold diagrams.
-
Strata in manifold diagrams are, indeed, manifolds (this is an immediate consequence of the framed conicality condition). However, more turns out to be true: strata have canonical smooth structures as well! This follows since strata inherit a classical framing (from the framing of the ambient Euclidean space), since all strata in manifold diagrams are PL manifolds (this roots in the theory behind point (1)), and since, by smoothing theory, framed PL manifolds have unique framed smooth structure.
-
Links of tubular neighborhoods in manifold diagrams (i.e. the stratifications with symbol ‘$l$’ in the earlier definition) are in fact well-defined: that is, there is, up to isomorphism, a unique choice of link at any given point of the diagram. This stands in contrast to classical topological conical stratifications, where non-homeomorphic choices of links exist.
-
Manifold diagrams have canonical geometric duals, in the sense of Poincaré duality). This duality relates manifold diagrams to so-called (framed) cell diagrams, which may then be considered as classical pasting diagrams (but with cells whose shapes generalize most of the familiar classes of shapes, such as ‘globular’, ‘simplicial’, or ‘opetopic’ shapes).
Let me dwell, and highlight once more, point (1) of the above list for a moment. It turns out that, as a consequence of (1), essentially all parts of the theory manifolds diagrams (i.e. their mappings, their neighborhoods, their links, their products, etc.) have canonical combinatorial counterparts in the theory of trusses—this quickly leads us on a path into a rich combinatorial world, which is explored in some detail in [3, Ch. 2] (and to which I also devoted (way too) many pages in my PhD thesis). As a consequence, manifold diagrams, unlike traditional manifolds, become computationally very tractable objects!
Diagrammatic computads and beyond
With the central definition of manifold diagams spelled out, let us begin to wrap things up and end this post by pointing out a few further directions of research (if you feel that this ending is premature, once more, I happily refer you to the extended version of this post!). Let’s start with a closer look at point (4) from the above list as it, too, entails an interesting story. The geometric duality of manifold and cell diagrams is parallel to (in fact, it is based on) a geometric duality in the theory of meshes, and consequently, at the level of framed fundamental posets, a categorical duality in the theory of trusses. The ‘dual meshes’ produced in this way turn out to be cell complexes: their cells are characterized by being both regular and carrying compatible framings—accordingly, they have been termed ‘framed regular cells’ in [3]. Dualizing the observation of manifold diagrams admitting canonical subdivisions into meshes, one finds that cell diagrams equally have canonical subdivisions into framed regular cell complexes (these are the ‘dual meshes’). However, this subdivision is a non-identity stratified map and it carries important information: it records which cells belong to the same stratum, or, in categorical terms, it records which cells are secretely degeneracies of lower dimensionsal cells. The ‘stratified encoding’ of degeneracies in this way may be a bit unfamiliar, but, together with the large shape class of framed regular cells, it has powerful consequences.
-
Isotopies of manifold diagrams are the tracks of stratified isotopies of manifold diagrams which are themselves manifold diagrams and do not contain point strata (an example is the ‘braid’, which is the track of an isotopy of two points embedded in the plane). It has been a long held intuition that such isotopies encode certain higher-categorical coherences. The translation underlying this intuition (from isotopies to higher-categorical laws) can be made fully precise via point (4): indeed, dualization translates isotopies to certain cell diagrams, which, after accounting for degeneracies, can then be cast as an equation between pasting diagrams. (It may be equally remarkable to note that the combinatorializability of manifold diagrams leads to a fully combinatorial theory of isotopies of manifold diagrams in the first place.) My favorite example of this process is the definition of categorical laws governing the sequence of categories, functors, natural transformations, modifications, … .
-
One may of course also consider ‘global’ directed higher structures simply by appropriately gluing together framed regular cells. The simplest, but also most instructive, such construction happens when we build our higher structures freely: this yields the case of diagrammatic computads. The definition of diagrammatic computads is exceedingly simply, as it need not follow the traditional inductive two-step procedure of building computads: indeed, usually one constructs computads inductively by, in the $n$th step, adding generating $n$-morphisms with boundary in existing $(n-1)$-morphisms, and then passing to the closure under composition and coherence conditions (which, passing back and forth between “new composites” and “new coherences” is often a pretty infinite process). In diagrammatic computads, this is process becomes unnecessary: boundaries of $n$-morphisms are manifold $(n-1)$-diagrams (or, if you work dually, cell $(n-1)$-diagrams) which already can express all the composites and isotopies you could possibly need. This makes diagrammatic computads really easy to work with.
The story of diagrammatic higher structures can be spun further in various ways, and active developement of its foundations is still underway. One direction that I wanted to highlight (in fact, asking David Corfield about this direction was the original motivation for writing the present blog post) is diagrammatic higher type theory: basically, the idea is to exploit the easiness of diagrammatic computads and their isotopy coherence laws in order to study the “internal language of the diagrammatic computad of all diagrammatic computads”. A hypothetical higher type theory of this kind could have interesting consequences, for instance, by demonstrating that $\Pi/\Sigma$ types can be internally constructed from a set of basic higher compositional principles (i.e. they need not be assumed as primitive rules). But, in only the last two sentences, we have gotten ourselves into rather speculative terrain!
Finally, one of my favorite and dearest parts of diagrammatic higher categorical thinking (which, at the same time, is also one of the most mysterious parts for me) is the role that invertibility and dualizability plays in it. Here, of course, the cobordism hypothesis finally comes into play: invertible morphisms are modelled not by manifold diagrams, but by so-called tangle diagrams—(omitting all details,) tangle diagrams are simply a variation of manifold diagrams in which we allow strata to ‘change directions’ with respect to the ambient framing. However, really, this set-up leads to a rather refined perspective on tangles as it provides a combinatorial framework for studying neighborhoods of ‘higher critical points’ (i.e. the points where tangles ‘change direction’). There is a tantalizing but mysterious connection of these critical points with classical differential $ADE$ singularities [2]: on one hand, classical singularities seem to resurface as ‘perturbation-stable’ singularities in tangle diagrams, on the other hand, the differential machinery breaks down (producing ‘moduli of singularities’) in high parameter ranges and this simply cannot happen in the combinatorial approach; put differently, the combinatorial approach must be better behaved than the differential approach in some way. Certainly, the ‘higher compositional’ perspective given through lens of diagrams is something that has no differential counterpart at all (and it leads to new interesting observations, such as a decomposition of the three-fold symmetric $D_4$ singularity link into a big bunch of binarily-paired-up singularities). But despite many ‘visible patterns’, most of this line of research remains completely unexplored (attempts of laying at least some foundations were made in [4])… but maybe that’s what I find so exciting about it. :-)
These are just a few of many directions you could pursue in studying diagrammatic higher categories. And I hope with time, the picture of how diagrammatic higher categories might contribute to the larger endeavours of current research in mathematics and physics will become clearer.
Acknowledgments
I would really like to take this opportunity to thank the hosts of the $n$-Category Café, which has been, and continues to be, a source of inspiration in manifold aspects of research and life. In particular, many of the ideas in diagrammatic higher category theory have been thought up by you. And many other ramblings have been very fun to read. (And while I’m at it, let me also give a shout out to the currently or formerly Oxford-based thinkers of diagrammatic higher categories: Christopher Douglas, Lukas Heidemann, André Henriques, David Reutter, Jamie Vicary, and many others, all of whose work has contributed to this area slowly emerging over the past few years).
An incomplete list of references
[1] Buoncristiano, Rourke and Sanderson. A geometric approach to homology theory. 1976
[2] Arnold. Normal forms for functions near degenerate critical points. 1972
[3] Dorn and Douglas. Framed combinatorial topology, Math. Surveys and Monographs, to appear (2025).
[4] Dorn and Douglas. Manifold diagrams and tame tangles. 2022.