Manifold diagrams: a geometric approach
Abstract. We describe the notion of manifold diagrams. Manifold diagrams generalize string diagrams to higher dimensions. Our focus will lie on giving an intuitively clear geometric description of these diagrams in terms of conical stratifications in a framed background space. We will also provide further details on the dual notion of pasting diagrams of computadic cells.
This note is part of a series.
UPDATE. Since writing this note, a new paper appeared, formally introducing manifold diagrams. The approach of the paper simplifies some of the ideas here, reducing them to two fundamental ingredients. Another paper relating to ideas beyond those ingredients, joint with Lukas Heidemann and Christopher Douglas, is in preparation.
Introduction
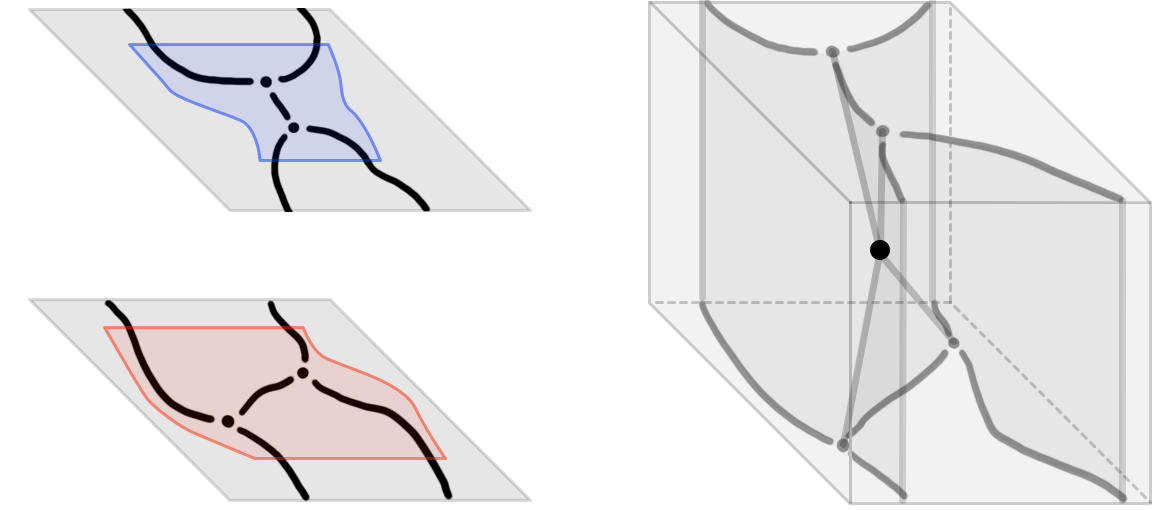
Manifold diagrams are the geometric duals of pasting diagrams of framed computadic cells, which we discussed in a previous note—while in the latter note we motivated the notion of framed computadic cells without defining it. In this note, by studying the geometry of manifold diagrams, we aim to give an actual (semiformal) definition of such computadic cells and their pasting diagrams. In Figure 1, we illustrate a manifold \(2\)-diagram together with its corresponding dual pasting diagram of framed computadic cells.

The idea of manifold \(n\)-diagrams (also called string diagrams in dimension \(n = 2\) and surface diagrams for \(n = 3\)) is long-known, and usually thought of as “intuitively clear”. A formalization of the idea has nonetheless been elusive. The case of string diagrams was explained early on by Joyal and Street [1], and the case of surface diagrams later by Trimble and others [2] [3] [4]. As speculated in [5], one issue in the formalization of manifold diagram in general dimension was that, traditionally, attempts towards a definition were made mainly in purely geometric terms; however, as duals to pasting diagrams, it is not surprising that there are combinatorial principles that govern the geometry of manifold diagrams.
We will here discuss both the geometric and the combinatorial approach to manifold diagrams (of course, both approaches turn out to be fully equivalent in a precise sense). Our approach will be based on ideas presented in ([6], Section 5.3) (and, relatedly, in ([5], Section S.1)).
The geometric approach
Manifold diagrams are stratifications
Manifold diagrams are, first and foremost, finite stratifications. Recall a finite prestratification \(f\) of a space \(X\) is a decomposition of that space into finitely many disjoint subspaces, also called strata. Every prestratification \(f\) comes with an entrance path preorder \(\Entr(f)\): this is the preorder whose objects are strata \(s\) of the stratification, with an arrow \(s \to t\) whenever the closure of \(s\) intersects \(t\) (the opposite of this preorder is called the “exit path preorder”). If \(\Entr(f)\) is a poset (i.e. a preorder without cycles), then we call \((X,f)\) a stratification (see [6], Appendix B, for a more in-depth discussion of (pre)stratifications).
Every finite stratification \(f\) of a space \(X\) has a continuous characteristic map to its entrance path poset, usually denoted by \(f : X \to \Entr(f)\): this maps points in a stratum \(s\) to the object \(s\) in the entrance path poset (the poset is given downward closed topology). A stratified map \(F\) between stratifications \((X,f) \to (Y,g)\) is a map of their underlying spaces \(X \to Y\) that descends to a map \(\Entr(F)\) of entrance path poset along their respective characteristic maps, that is, the following commutes:
\[\begin{CD} X @>{F}>> Y\\ @VVV @VVV \\ \Entr(f) @>{\Entr(F)}>> \Entr(g). \end{CD}\]A manifold \(n\)-diagram is a “framed conical” stratification of the open \(n\)-cube \(\mathbb{I}^n = (-1,1)^n\) (or rather, of the \(n\)-globe as we will explain). Before making the condition of “framed conicality” precise, we will discuss framed maps and framed cones.
Framed stratified maps
Framed stratified maps must preserve the “categorical directions” of the \(n\)-cube \(\mathbb{I}^n\) as follows. A stratified map \(F\) of stratifications of \(\mathbb{I}^n\) is called framed if its underlying map \(F : \mathbb{I}^n \to \mathbb{I}^n\) has the following property: for each \(k \leq n\), \(F\) factors through the projections \(\pi_{\leq k} : \mathbb{I}^n \cong \mathbb{I}^k \times \mathbb{I}^{n-k} \to \mathbb{I}^k\) by a map \(F_k\), i.e. such that the following commutes:
\[\begin{CD} \mathbb{I}^n @>{F}>> \mathbb{I}^n\\ @V{\pi_{\leq k}}VV @VV{\pi_{\leq k}}V \\ \mathbb{I}^k @>{F_k}>> \mathbb{I}^k. \end{CD}\]The notion of “framed” maps equally applies to other objects defined by \(n\)-fold products (in particular, the closed unit \(n\)-cube, as we will shortly come back to).
Framed (double) cones
A manifold \(0\)-diagram is the unique stratification of the point \(\mathbb{I}^0\). Manifold \(n\)-diagrams are defined mutually inductively with so-called manifold \(n\)-singularities: these describe the “small” open neighborhoods around point strata in manifold diagrams (for example, the stratification on the right in Figure 3 is a manifold \(3\)-singularity: it captures a \(3\)-dimensional neighborhood around the central point stratum). Formally, manifold \((n+1)\)-singularities will shortly be defined by taking the framed double cone of two manifold \(n\)-diagrams with equal framed boundary; framed boundaries are obtained by taking boundaries of framed closures of manifold diagrams. The relevant terms (framed closures, boundaries, cones, and double cones) are defined as follows.
A framed closure of a stratification \(f\) of the open unit \(n\)-cube \(\mathbb{I}^n\) is a stratification \(\bar f\) of the closed unit \(n\)-cube \(\textbf{I}^n = [-1,1]^n\) together with framed stratified maps \(\bar f \hookrightarrow f \hookrightarrow \bar f\) such that:
-
on underlying spaces, the first map is an inclusion \(\textbf{I}^n \hookrightarrow \mathbb{I}^n\) and the second map is the canonical inclusion \(\mathbb{I}^n \hookrightarrow \textbf{I}^n\),
-
on entrance path posets, the maps are inverse isomorphisms of posets.
A framed boundary \(\partial f\) of \(f\) is a stratification of the \(n\)-cube boundary \(\partial \textbf{I}^n\) obtained by restricting a framed closure \(\bar f\) of \(f\) to \(\partial \textbf{I}^n\) (implicit in the choice of a framed boundary is therefore the choice of a framed closure).
Given a stratification \(f\) with framed boundary \(\partial f\), then the framed cone \(\mathrm{Cone}(f)\) is the stratification of \(\mathbb{I}^{n} \times [0,1)\) obtained by restricting the stratification of \(\textbf{I}^n \times [0,1]\) given by linearly shrinking the closure \(\bar f\) of \(f\) into a new point singularity at \(0\)—we illustrate this in Figure 2.

Given two stratifciations \(f\), \(g\) with equal framed boundaries \(\partial f\), \(\partial g\), their framed double cone \(\mathrm{DblCone}(f,g)\) is the stratification of the \((n+1)\)-cube \(\mathbb{I}^{n+1} = \mathbb{I}^{n} \times \mathbb{I}\) obtained by gluing together the two framed cone stratifications of \(f\) respectively \(g\) in the obvious way.
Defining manifold diagrams and singularities
The inductive definition now proceeds as follows. As mentioned already, manifold \(0\)-diagrams are pretty trivial. Inductively, assume to have defined those stratifications of \(\mathbb{I}^n\) that are manifold \(n\)-diagrams.
A manifold \((n+1)\)-singularity is a stratification of \(\mathbb{I}^{n+1}\) obtained as the double cone of two manifold \(n\)-diagrams with equal framed boundaries. As an example, the stratification of \(\mathbf{I}^3\) in Figure 3 is a manifold \(3\)-singularity.
A manifold \((n+1)\)-diagram is a stratification \(f\) of \(\mathbb{I}^{n+1}\) such that the following holds. Firstly, each point \(x \in \mathbb{I}^{n+1}\) has a framed neighborhood \(U_x : \mathbb{I}^{n+1} \hookrightarrow \mathbb{I}^{n+1}\) on which the stratification restricts to a stratification \(f_x\) that is framed stratified homeomorphic to a stratification of product form \(c_x \times \mathbb{I}^{n+1-k}\) where \(c_x\) is a manifold \(k\)-singularity, \(k \leq n+1\). Secondly, the stratification has a boundary \(\partial f\) that restricts on \(\partial \textbf{I}^n \times \textbf{I}\) to a stratification of product form \(g \times \textbf{I}\) (where \(g\) is some stratification of \(\partial \textbf{I}^n\)). We usually refer to the first condition as framed conicality, and to the second condition as globularity.
Remark 1 (Framed conicality). The framed conicality condition is of course a “framed” adaptation of the usual definition of conical stratification (see ([7], Section A.5)).
Remark 2 (Strict globularity). The globularity condition is more stringent than it needs to be (meaning there are stratifications that deserve to be called manifold diagrams and which do not satisfy the condition; however, each such stratification will be framed stratified homeomorphic to a manifold diagram in the sense defined above). We chose the stricter condition for simplicity.
Globularity equivalently says that (closures of) manifold diagrams can be obtained by pullbacks along the usual quotient map \(\textbf{I}^n \to \textbf{G}_n\) of the \(n\)-cube \(\textbf{I}^n\) to the \(n\)-globe \(\textbf{G}_n\). This then leads to the slogan “manifold diagrams are framed conical stratifications of the \(n\)-globe”.
Remark 3 (Tameness). We have omitted from our discussion one detail needed in the definition of manifold diagrams: namely, manifold diagrams are not merely stratifications of the \(n\)-cube but they are required to be flat framed stratifications as defined in ([6], Chapter 5). Technically, this means that any manifold diagram must be refinable by a mesh (a finite stratification of “framed” open disk strata). Heuristically, this is a tameness condition: it avoids “infinitely many wiggles in the wrong places”. An example of non-tame behaviour can be found in the discussion of tame tangles.
The combinatorial approach
Importantly, manifold diagrams live a double life: there are not only geometric objects but also combinatorial ones. Formally, the combinatorialization of manifold diagrams relies on the combinatorialization of flat framed stratifications (which is spelled out in ([6], Chapter 5), see also Remark 3 above). Here, we will only outline the underlying idea.
Manifold diagrams as structured poset bundle towers
The notion of “stratified bundles” generalizes fiber bundles to the stratified context: fibers may be stratified, and local trivializations are only required over each base stratum separately (meaning fibers can change when passing between strata). Given a manifold \(n\)-diagram \(f\) of the open \(n\)-cube \(\mathbb{I}^n\), the tower of projections \(\pi_i : \mathbb{I}^i = \mathbb{I}^{i-1} \times \mathbb{I} \to \mathbb{I}^{i-1}\) (for \({1 \leq i \leq n}\)) starting at \(\mathbb{I}^n\), can be canonically endowed with the structure of stratified bundles \(\pi_i : M^f_i \to M^f_{i-1}\) where \(M^f_i\) are stratifications of \(\mathbb{I}^i\) and \(M^f_n\) is finer than \(f\). (Technically, these bundles are required to have a further property, called “constructibility”). In Figure 4, for the manifold diagram \(f\) on the left, we illustrate a resulting tower of stratified bundles \(M^f_2 \to M^f_1 \to M^f_0\) on the right; note that \(M^f_2\) is indeed finer than \(f\).
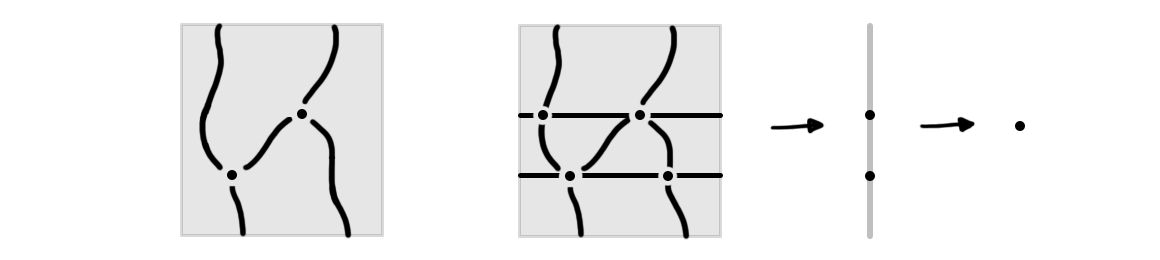
The combinatorialization of manifold diagram \(f\) can be obtained by passing to the entrance path poset tower of such towers of stratified bundles \(M^f_i \to M^f_{i-1}\), i.e. the tower consisting of “poset bundles” \(\Entr(M^f_i \to M^f_{i-1})\). Such poset bundles are introduced in ([6], Chapter 2) under the name \(1\)-truss bundles. Their fibers, called \(1\)-trusses, are certain structured zig-zag posets. A tower of \(n\) consecutive \(1\)-truss bundles (ending in the point) defines an \(n\)-truss. Each manifold diagram \(f\) corresponds, up to framed stratified homeomorphism, to a unique stratified \(n\)-truss (where the \(n\)-truss itself is defined by the bundles \(\Entr(M^f_i \to M^f_{i-1})\), and the additional “stratification” structure records the entrance path poset map \(\Entr(M^f_n \to f)\) of the refinement \(M^f_n \to f\)). We omit further discussion of the combinatorial notion of (stratified) \(n\)-trusses here since trusses deserve their own note.
Dualizing poset bundle towers
We now we briefly sketch how the above combinatorial definition of manifold diagrams can be formally dualized to a combinatorial definition of pasting diagrams (of framed computadic cells).
The geometric duals of manifold \(n\)-diagrams are exactly pasting \(n\)-diagrams of framed computadic cells. Formally, this dualization simply dualizes all pieces in the combinatorial datum of a manifold diagram. We outline the following interpretation of the dual datum.
-
Firstly, we pass to opposite posets in the tower of poset bundles \(\Entr(M^f_i \to M^f_{i-1})\) associated to a given manifold \(n\)-diagram \(f\) (as described above). The first poset \(\Entr(M^f_n)^{\mathrm{op}}\) in the resulting tower can be interpreted as the face poset of a regular cell complex, and subsequent posets as the face posets of “projections” of this cell complex. The tower thus defines a notion of “structured” regular cell complex: this is called a flat framed regular cell complex (see ([6], Section 1.3)).
-
Secondly, the map \(\Entr(M^f_n \to f)^{\mathrm{op}}\) (of opposite entrance path posets) yields a map from the face poset of the cell complex to the opposite poset \(\Entr(f)^{\mathrm{op}}\). In fact, this poset map is a quotient map of posets (technically, it is a connected-quotient map as introduced in ([6], Appendix B)). Morally, the quotient indicates the position of degeneracies in the resulting pasting diagram.
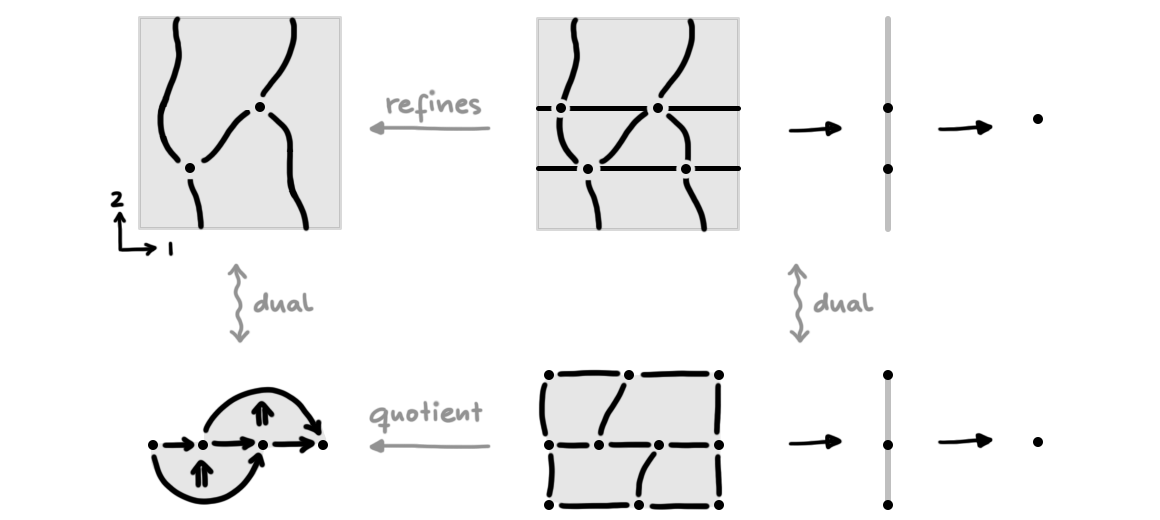
The steps of the dualization process are illustrated in Figure 5: the first row shows a manifold \(2\)-diagram \(f\) together with its associated tower of stratified bundles \(M^f_i \to M^f_{i-1}\), while the second row shows the dual pasting diagram together with its associated tower of projections of cell complexes (that is, we illustrate the posets \(\Entr(M^f_i)^{\mathrm{op}}\) by their corresponding regular cell complexes).
In summary, pasting diagrams of framed computadic cells can be understood as certain quotients of flat framed regular cell complexes.
Remark 4. Importantly, note that the data of a pasting diagram of computadic cells is given by a quotient map from a flat framed regular cell complex (in particular, a pasting diagram is not just the codomain of that quotient). For convenience, this quotient map may be represented in a single diagram by indicating where the quotient “happens”: for instance, the pasting diagram of framed computadic cells in Figure 5 is meant to be equivalently represented by the earlier pasting diagram in Figure 1.
In the special case that a manifold \(n\)-diagram is a manifold \(n\)-singularity, its dual pasting diagram will be a single framed computadic \(n\)-cell (given by a quotient of a single framed regular \(n\)-cell). The fact that we defined manifold diagrams and manifold singularities in a mutually inductive fashion mirrors the observation that cell diagrams and cells also have a mutually inductive relationship: indeed, each pasting \((n+1)\)-diagram is made of \((n+1)\)-cells, and each \((n+1)\)-cell carries pasting \(n\)-diagrams in its domain and codomain.
Manifolds vs cells
It may be worth emphasizing the following: manifold diagrams are fully equivalent to pasting diagrams (of framed computadic cells) as discussed above. However, the former notion offers the following moral advantage over the latter notion. The refinement \(M^f_n \to f\) associated to a manifold \(n\)-diagram \(f\) is determined by the stratification \(f\) itself (i.e. the codomain of the refinement). In contrast, the quotient map defining a pasting diagram is in general not determined by its codomain. This means that the quotient map “forgets” data for the pasting diagram; this data encodes compositional “weakness” which can lead to the problem of undefinability of computadic shapes as outlined in a previous note.
References
[1] “The geometry of tensor calculus, I”, Joyal + Street
[2] “Surface diagrams”, Trimble
[3] “Gray Categories with Duals and their Diagrams”, Barrett + Meusburger + Schaumann
[4] “Surface diagrams for Gray-categories”, Hummons
[5] “Associative \(n\)-categories”, Dorn
[6] “Framed combinatorial topology”, Dorn + Douglas
[8] “Manifold diagrams and tame tangles”, In preparation, see here for updates
