Paradigms of higher category theory

<! --- LETTERS ---> $$ \newcommand{\lR}{\mathbb{R}} $$ $$ \newcommand{\lZ}{\mathbb{Z}} $$ $$ \newcommand{\lN}{\mathbb{N}} $$ $$ \newcommand{\lI}{\mathbb{I}} $$ $$ \newcommand{\II}{\mathbb{I}} $$ $$ \newcommand{\bI}{\mathbf{I}} $$ $$ \newcommand{\bC}{\mathbf{C}} $$ $$ \newcommand{\bD}{\mathbf{D}} $$ $$ \newcommand{\bE}{\mathbf{E}} $$ $$ \newcommand{\bF}{\mathbf{F}} $$ $$ \newcommand{\iI}{\mathsf{I}} $$ $$ \newcommand{\iA}{\mathsf{A}} $$ $$ \newcommand{\iB}{\mathsf{B}} $$ $$ \newcommand{\iC}{\mathsf{C}} $$ $$ \newcommand{\iD}{\mathsf{D}} $$ $$ \newcommand{\iE}{\mathsf{E}} $$ $$ \newcommand{\iF}{\mathsf{F}} $$ $$ \newcommand{\iM}{\mathsf{M}} $$ <! --- SYMBOLS ---> $$ \newcommand{\eps}{\epsilon} $$ $$ \newcommand{\SetCat}{\mathrm{Set}} $$ $$ \newcommand{\Bool}{\mathrm{Bool}} $$ $$ \newcommand{\Pos}{\mathrm{Pos}} $$ $$ \newcommand{\lbl}{\mathsf{lbl}} $$ $$ \newcommand{\subdiv}{\mathsf{sd}} $$ $$ \newcommand{\Hom}{\mathrm{Hom}} $$ $$ \newcommand{\Fun}{\mathrm{Fun}} $$ $$ \newcommand{\Psh}{\mathrm{PSh}} $$ <! --- OPERATORS ---> $$ \newcommand{\dim}{\mathrm{dim}} $$ $$ \newcommand{\id}{\mathrm{id}} $$ $$ \newcommand{\src}{\partial^-} $$ $$ \newcommand{\tgt}{\partial^+} $$ $$ \newcommand{\und}[1]{\underline{#1}} $$ $$ \newcommand{\abs}[1]{\left|{#1}\right|} $$ $$ \newcommand{\op}{^{\mathrm{op}}} $$ $$ \newcommand{\inv}{^{-1}} $$ <! --- CATEGORIES, FUNCTORS AND CONSTRUCTIONS ---> $$ \newcommand{\ttr}[1]{\mathfrak{T}^{#1}} $$ $$ \newcommand{\lttr}[2]{\mathfrak{T}^{#1}{(#2)}} $$ $$ \newcommand{\truss}[1]{\mathsf{T}\!\mathsf{rs}_{#1}} $$ $$ \newcommand{\sctruss}[1]{\bar{\mathsf{T}}\!\mathsf{rs}_{#1}} $$ $$ \newcommand{\rotruss}[1]{\mathring{\mathsf{T}}\!\mathsf{rs}_{#1}} $$ $$\newcommand{\trussbun}[1]{\mathsf{TrsBun}_{#1}} $$ $$ \newcommand{\trusslbl}[1]{\mathsf{Lbl}\mathsf{T}\!\mathsf{rs}_{#1}} $$ $$ \newcommand{\blcat}[1]{\mathsf{B}\mathsf{lk}_{#1}} $$ $$ \newcommand{\blset}[1]{\mathsf{Blk}\mathsf{Set}_{#1}} $$ $$ \newcommand{\fcl}[2]{\chi^{#1}_{#2}} $$ $$ \newcommand{\Entr}{\mathsf{Entr}} $$ $$ \newcommand{\Exit}{\mathsf{Exit}} $$ <! --- ARROWS AND RELATIONS ---> $$ \newcommand{\fleq}{\preceq} $$ $$ \newcommand{\fles}{\prec} $$ $$ \newcommand{\xto}[1]{\xrightarrow{#1}} $$ $$ \newcommand{\xot}[1]{\xleftarrow{#1}} $$ $$ \newcommand{\ot}{\leftarrow} $$ $$ \newcommand{\toot}{\leftrightarrow} $$ $$ \newcommand{\imp}{\Rightarrow} $$ $$ \newcommand{\iff}{\Leftrightarrow} $$ $$ \newcommand{\iso}{\cong} $$ $$ \newcommand{\into}{\hookrightarrow} $$ $$ \newcommand{\proto}{\longrightarrow\mkern{-2.8ex}{\raisebox{.3ex}{$\tiny\vert$}}\mkern{2.5ex}} $$ <! --- DIAGRAM ARROWS ---> <! ---... should replace \rlap by \mathrlap, see KaTeX doc ---> $$ \newcommand{\ra}[1]{\xrightarrow{\ \ #1\ \ }\phantom{}\kern-1.5ex} $$ $$ \newcommand{\la}[1]{\xleftarrow{\ \ #1\ \ }\phantom{}\kern-1.5ex} $$ $$ \newcommand{\da}[1]{\downarrow\raisebox{.5ex}{\rlap{$\scriptstyle#1$}}} $$ $$ \newcommand{\dra}[1]{\raisebox{.2ex}{\llap{$\scriptstyle#1$}}\kern-.5ex\searrow}} $$ $$ \newcommand{\dla}[1]{\swarrow\kern-1ex\raisebox{.2ex}{\rlap{$\scriptstyle#1$}}} $$ $$ \newcommand{\ua}[1]{\uparrow\raisebox{.2ex}{\rlap{$\scriptstyle#1$}}} $$ $$ \newcommand{\ura}[1]{\raisebox{.2ex}{\llap{$\scriptstyle#1$}\kern-.5ex\nearrow}} $$ $$ \newcommand{\ula}[1]{\nwarrow\kern-1ex\raisebox{.2ex}{\rlap{$\scriptstyle#1$}}} $$

Abstract. We explore two fundamental paradigms underlying models of higher categories. Most models for higher categories are based on the paradigm of contraction; this requires spaces of evaluations of a single pasting diagram to be contractible. The paradigm, however, generally fails to yield easy descriptions of interesting non-contractible behaviour in spaces of composites. This is remedied by working instead with the paradigm of isotopy as we will explain.

This note is part of a series.

Introduction

A goal of algebraic topology and higher category theory is to understand the “coherent character” of space in algebraic terms. Tackling this goal means to distill combinatorial rules for when composites of (higher) paths in spaces “cohere”. Here we discuss two paradigms for the construction of such combinatorial coherence rules: the paradigm of “contraction” and that of “isotopy” (the latter also referred as the “manifold-diagrammatic paradigm”). They may be summarized as follows.

• Contraction paradigm. A coherence between two $n$-diagrams can be constructed as a sequence of “contractions”; a contraction is an $(n+1)$-cell between two $n$-diagrams that exists whenever both diagrams can be obtained as evaluations of another $n$-diagram.
• Isotopy/manifold-diagrammatic paradigm. A coherence between two $n$-diagrams can be constructed by giving an $(n+1)$-diagram between them which is an isotopy, meaning it must not contain any non-degenerate $(n+1)$-cells (in manifold-diagrammatic terms, this says all strata are of dimension $k > 0$).

We note immediately that the two paradigms are rather different in their nature: the contraction paradigm is phrased as a condition of existence of structure (namely, of contractions). The isotopy paradigm is phrased as a description of existing structure. More importantly, the contraction paradigm describes coherences directly only in a “local” (contractible!) space of contractions, whereas from the perspective of the isotopy paradigm one studies coherences on a “global” level. We now explain each of the two ideas in more detail.

The contraction paradigm

The idea of contractions, in one form or another, powers most models of higher categories that are currently in use. It may be traced back at least to Grothendieck ([1], Section 1-13).

Description

As outlined above, the contraction paradigm enforces there to be coherence cells (also called contractions) between any two evaluations of the same pasting diagram. More precisely, such coherence cells should be regarded themselves as “higher” evaluations of that same pasting diagram; and this in turn allows for such coherences to be themselves related by yet higher coherences (by applying again the paradigm of contraction). As a result, the “space” of all evaluations of a given pasting diagram (which now includes coherences as paths, and higher coherences as higher paths) becomes a contractible space. A popular variation of contraction is obtained by taking the latter observation to be the primary condition; that is, to require the space of evaluations to be contractible.

Example

At the center of Figure 1 we depict a pasting \(2\)-diagram consisting of four cells; one cell is labeled by “\(\alpha\)”, one by “\(\beta\)”, while the other two are degenerate cells (marked by the label “\(\mathrm{id}\)”)—as we will revisit shortly, the availability of degenerate cells in pasting diagrams is fundamental for the correct description of coherences.

Figure 1. A coherence between different evaluations of a pasting diagram.

Both to the left and the right of the pasting diagrams we indicated two evaluations: in each case we first “associate” cells into a given order of evaluation (indicated by circles in blue and red respectively) and then evaluate in that order. The paradigm of contraction now dictates that there will be a contraction \(3\)-cell witnessing a coherence between the two resulting \(2\)-cells.

The isotopy paradigm

Isotopies are a long known heuristic for thinking about coherences. It frequently appears in the context of TQFTs, the generalized tangle hypothesis, and (relatedly) in applications of the Pontryagin-Thom construction. In each of these cases, the idea is that coherences appear as deformations of manifold geometries (we will see an example shortly). Unfortunately, such “manifold geometry deformations” have previously been hard to phrase formal mathematical terms. The notion of manifold diagrams provides the technology needed to make the idea precise.

Description

As outlined above, the isotopy paradigm is simply the description of a certain subclass of pasting diagrams. Namely, a pasting \(n\)-diagram (of framed computadic cells) is called a coherence (or, more distinctly, an \(n\)-isotopy) between its domain and codomain pasting \((n-1)\)-diagram if it does not contain non-degenerate \(n\)-cells.

Since manifold diagams are the duals of pasting diagrams, this definition of isotopies applies equally (but with “dualized” dimensions) to the case of manifold diagrams: namely, the absence of non-degenerate \(n\)-cells in a pasting diagram \(n\)-isotopy translates into the absence of \(0\)-strata (i.e. point strata) in the manifold \(n\)-diagram dual to that isotopy. In other words, a manifold \(n\)-diagram is a isotopy if it does not contain manifold \(n\)-singularities.

Recall that manifold diagrams are framed conical stratifications. The framed conicality condition together with the absence of point strata implies precisely that there are no “local changes” in topology when traveling from the domain to the codomain of a manifold diagram isotopy. This recovers the classical intuition that categorical coherences are “continuous deformations” of manifold geometries.

Example

In Figure 2 on the left we depict a manifold diagram that is an isotopy: it takes two point singularities and continuously deforms them by rotating them around each other. On the right, we depict a manifold diagram that is not an isotopy: it contains a singularity at which a bifurcation happens (and thus the local topology changes).

Figure 2. An isotopy and a non-isotopy manifold diagram.

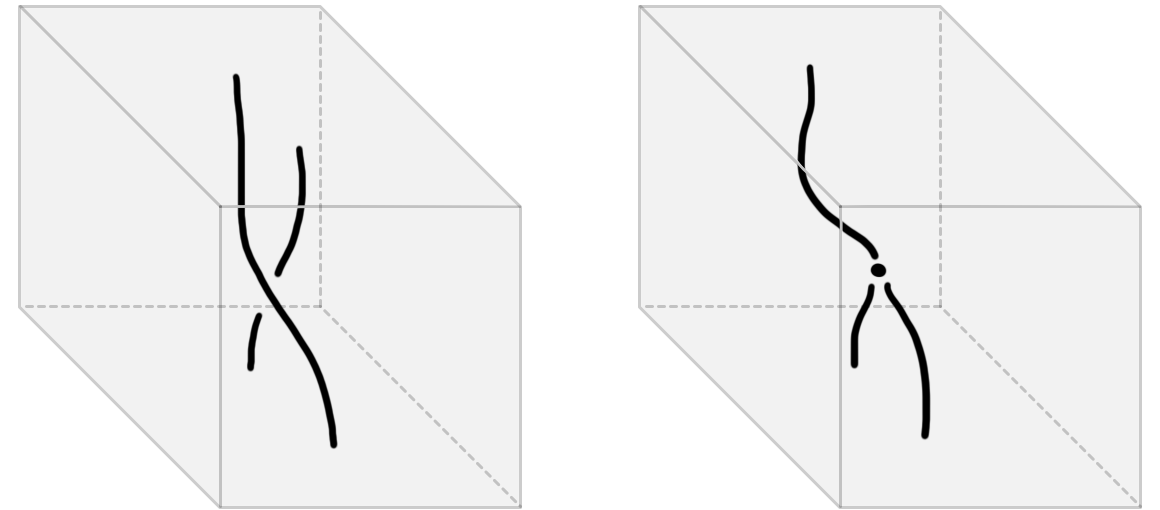
In Figure 3 we depict the pasting \(3\)-diagrams that are dual to the manifold diagrams in Figure 2. The right “diagram” is simply a non-degenerate \(3\)-cell (dualizing the point stratum on the right in Figure 2). The left cellular pasting diagram is, as indicated, the pasting of two 3-cells—the diagram also appeared as Figure 7 in our discussion of framed computadic cells, where we explained that each of these cells is in fact a degenerate cell. This makes the left pasting diagram an isotopy as claimed. In contrast, the right pasting \(3\)-diagram contains a non-identity \(3\)-cell and is thus not an isotopy.

Figure 3. An isotopy and a non-isotopy pasting diagram of framed computadic cells.

Comparison

Heuristics

On the face of it, the paradigm of isotopy has a more tangible topological interpretation: an isotopy, i.e. a coherence diagram in the isotopy sense, is precisely a deformation of a manifold diagram in a topological sense.

In contrast, this topological interpreation does not immediately carry over to case of contractions, i.e. coherence cells in the contraction sense. To (heuristically) understand the relation we must instead decompose topological coherences into sequences of “smaller” deformations, each of which may be understood as a “perturbation”. Namely, “evaluating away” a degenerate cell removes the space taken by that degenerate cell. The inverse process, of inserting space, allows to interpret contractions as perturbations. A general deformation may then be understood as a zig-zag of such perturbations, that “remove” and “insert” space.

For the braid coherence shown earlier in Figure 2 (and its corresponding isotopy of pasting diagram shown in Figure 3), we illustrate the corresponding chain of contractions respectively the zig-zag of corresponding perturbations in Figure 4.

Figure 4. A chain of contractions describing the braid.

Conclusion

In conclusion, whether using “contraction” or “isotopy” as guiding paradigms when defining higher categories, we should ultimately arrive at equivalent models. Nonetheless, the underlying ideas of the two paradigms are quite different, with (at least) the following implications.

• Condition vs description. The contraction paradigm forces existence of contraction cells, which introduces new terms in models of higher categories that one needs to be able to compute with. This makes working with small examples (see [2]) of higher categories hard. In contrast, no new terms are needed when working with isotopies. Instead, we solely rely on cell shapes being general enough (namely, computadic) in order to be able to describe coherences as certain pasting diagrams themselves. This requires more thought to initially set up (since setting up computadic shapes is harder than setting up, say, simplices) but it makes it easier to work with higher coherences later on (in particular providing access to small examples of higher categories).

• Globality. While contractions may be assembled into “global” deformations as discussed above (see Figure 4), there is usually no good combinatorial framework for working with such composite contractions: the reason is that these composites usually cannot be described as evaluations a single “global” pasting diagram (instead the pasting diagrams describing the individual contractions in the composite may be incommensurable). In contrast, the isotopy paradigm is tailored for the study of global deformations, and the class of such deformations has rich structure in itself, providing insights into the “coherent character” of space.

Remark. In the context of working with small examples Jacob Lurie writes:

a formalism which would allow you to compute easily with small examples should give you a recipe for calculating unstable homotopy groups of spheres. (Of course, this depends on exactly what you mean by “small.”)

Any attempt of “calculation” aside, implementing the isotopy paradigm at least gives a recipe for writing down elements of unstable homotopy groups of spheres very neatly as categorical pasting diagrams: that is, pasting and manifold diagram can naturally express representatives of homotopy groups. This observation leads to a “categorical” version of the Pontryagin-Thom construction, which recasts the classical result in purely combinatorial recasting using the technology of computadic cells and manifold diagrams; the construction, however, is very much its own story!

References

[1] “Pursuing Stacks”, Grothendieck

[2] “Confessions of a Higher Category Theorist”, Shulman, Blog post